Table of Contents
All my notes
Gold
What is the fascination with gold?
It is an interesting material. It doesn't react chemically and therefore doesn't oxidize or degrade over time. It has high electrical conductivity as well as good optical reflectivity in infrared. It is malleable and easily worked and reworked. However it's importance and current value is more due to the cultural place it fills rather than a technical one in the modern world.
The lack of chemical reactivity, it could be argued, gives it a sense of permanency which is a rare thing in an ever changing world. It has been seen therefore as a constant store of value since ancient times. The idea of having gold for the days of Armageddon when modern society breaks down and all Fiat currency becomes worthless seems dubious to me. If I have a gold bar in my house in our current modern, functional society in peacetime, it is still not a trivial thing to get this converted into goods I can actually use (food, clothing, shelter etc..). First of all, you have to prove in some way that the material you have is actually gold. This requires assaying it in some way. Then you need to find someone to accept this block of metal and exchange it for something that is of actual use to you. In our current fully functional society, where all services and systems are running as normal, this is still not trivial. How would this look like in some type of post apocalyptic world where nothing is running or working? How many willing takers are there going to be for the block of metal in exchange for the rare food / clothing etc… they may be in possession of ?
What is the point in the trade in gold? As someone once said,1) from the perspective of an extra-terrestrial visiting our planet, you have one set of people investing a lot of effort in digging up and gathering this material in one part of the world, then transporting it with a great security effort to another part of the world to deposit it in another hole in the ground and then sit around guarding it. This does not have any positive economic impact for anybody. Nothing has been made, produced or accomplished in this exercise.
BUT, as long as people view gold as being a safe haven asset, then it becomes a self fulfilling prophecy and so long as people react in this way in their handing of gold, then it will fulfill this purpose. This does sound more due to the confidence level people place in the material rather than inherent value. This then starts to be similar to the paper currency risk, whose value is also based on confidence levels in governments that people think they are guarding against.
~~DISCUSSION~~
Erdős Number
In the world of mathematics, you can see networking effects in terms of your Erdős number which quantifies the series of connections through the scientific community to the published work of Paul Erdős. As well as being a prolific author of mathematical papers, Paul Erdős was also quite an enigmatic character. His biography, The Man Who Loved Only Numbers, is worth a read.
To be assigned an Erdős number, one must be a coauthor of a research paper with another person who has a finite Erdős number. Paul Erdős has an Erdős number of zero. Anybody else's Erdős number is $k + 1$ where $k$ is the lowest Erdős number of any co-author.
Erdős wrote around 1,500 mathematical articles in his lifetime, mostly co-written. He had 511 direct collaborators; these are the people with Erdős number 1. The people who have collaborated with them (but not with Erdős himself) have an Erdős number of 2 (9267 people as of 2010), those who have collaborated with people who have an Erdős number of 2 (but not with Erdős or anyone with an Erdős number of 1) have an Erdős number of 3, and so forth. A person with no such coauthorship chain connecting to Erdős has an Erdős number of infinity (or an undefined one). Since the death of Paul Erdős, the lowest Erdős number that a researcher can obtain is 2. 2)
Below is the distribution of Erdős Numbers3)
Erdös number 0 --- 1 person
Erdös number 1 --- 504 people
Erdös number 2 --- 6593 people
Erdös number 3 --- 33605 people
Erdös number 4 --- 83642 people
Erdös number 5 --- 87760 people
Erdös number 6 --- 40014 people
Erdös number 7 --- 11591 people
Erdös number 8 --- 3146 people
Erdös number 9 --- 819 people
Erdös number 10 --- 244 people
Erdös number 11 --- 68 people
Erdös number 12 --- 23 people
Erdös number 13 --- 5 people
My Erdős Number would appear to be 5
Erdős Number 5
Checking through AMS:
http://www.ams.org/mathscinet/collaborationDistance.html
Path 1
O'Brien-Huyet/McInerney-Pokrovskii-Boltyanskii-Soifer-Erdős
“Rigorous analysis of complicated behaviour in a truncated LangKobayashi model”
O. Rasskazov, G. Huyet, J. Mcinerney, A. Pokrovskii
- Alexei V. Pokrovskii coauthored with Vladimir Grigorʹevich Boltyanskii MR0862446 (88a:93001)
- Vladimir Grigorʹevich Boltyanskii coauthored with Alexander Soifer MR1104655 (92f:52031)
- Alexander Soifer coauthored with Paul Erdős1 MR1214695
Path 2
Stephen Barnett is same or??
Huyet-Barnett-Johnson-Schönheim-Erdős
Superposition states at finite temperature
G. Huyet, S Franke-Arnold, S.M. Barnett
- Stephen Barnett coauthored with Charles R. Johnson MR0943760 (89c:15005)
- Charles R. Johnson coauthored with Johanan Schönheim MR0705965 (84j:15007)
- Johanan Schönheim coauthored with Paul Erdős1
Path 3
Arlazarov, V. L.; Uskov, A. V. Faradžev, I. A. An algorithm for finding all simple cycles in a directed graph. (Russian) Studies in discrete mathematics (Russian), pp. 178–183. Izdat.“Nauka'', Moscow, 1973.
MR Erdos Number = 4
- A. V. Uskov coauthored with I. A. Faradzhev MR0412019 (54 #148)
- I. A. Faradzhev coauthored with Mikhail H. Klin MR0617203 (82g:20012)
- Mikhail H. Klin coauthored with Peter J. Cameron MR1920405 (2003f:20001)
- Peter J. Cameron coauthored with Paul Erdős1 MR1106651 (92g:11010)
Path 4
MR2070618 34C23 (34C25 34K13 34K18) Krasnoselʹskii, A. M.; McInerney, J.; Pokrovskii, A. V. Synchronized double-frequency oscillations in a class of weakly resonant systems. Nonlinear Anal. 57 (2004), no. 7-8, 929–949.
MR Erdos Number = 4
- J. G. McInerney coauthored with Alexander M. Krasnoselʹskii MR2070618
- Alexander M. Krasnoselʹskii coauthored with Vladimir Grigorʹevich Boltyanskii MR0862446
- Vladimir Grigorʹevich Boltyanskii coauthored with Alexander Soifer MR1104655
- Alexander Soifer coauthored with Paul Erdős1 MR1214695
Erdős Number 4 ?
tool From Microsoft would suggest Erdös number of 4 McInerney-H.S.Gamble-H.L.Montogmery-Erdős
doesn't look reliable though, results don't make sense.. (McInerney search does not show this link!)
~~DISCUSSION~~
Emacs & Macros
Looking again at my old text editor Emacs and what it can do with Emacs lisp. Lisp expresses everything in terms of lists and the editor itself is written in this and can be modified and extended using it. Watched some of Emacs Rocks videos and it is quite amazing what you can do if you can become fluent in this environment. Then again, the amount of time you need to invest to reach that level of proficiency is enormous. The number and functions and key bindings involved is huge
 4)
4)
Under Alternative Text for this comic: “Real programmers set the universal constants at the start such that the universe evolves to contain the disk with the data they want.” - May br right if the Simulation_hypothesis is true.
Anyways, this brought me on to the topic of Keyboard macros that makes it easy to string together actions in Emacs
<F3> record, Complete long list of Emacs “Keyboard Yoga” <F4> to stop M-x kmacro-call-macro to run the sequence automatically optionally tie the macro to a keybinding.
… and then onto Excel Macros — which may actually help me do some routine data entry tasks automatically. This, however, also seems to require some time needed to implement across a series of excel files.
“Computers can help you do everything more quickly… it just takes longer.”
~~DISCUSSION~~
Currency Variation & Stock Price
Stock prices are discussed a lot. Currencies a lot less - though variations can be equally dramatic. The Euro has held values as priced in US dollars from a minimum of 0,84\$ in Nov 2000 up to 1.6\$ July 2008. At the time of writing it is priced at 1.17\$ which is similar to valuation at launch in Jan 1999. The short term variations can be equally dramtic.
In the year to date, the € as priced in \$ has risen by around 10%. Significantly, at least to me, this mirrors exactly the “rise” of the SP500 in this time frame. Priced in € the SP500 has completely stalled in the first 6 months of 2017. The SP500 is, however, priced in \$ and as such is nominally doing perfectly well in 2017. No major alarm about a stalling US stock market. The 10% depreciation of the $ in € terms is also notable absent from headlines.
Gyrations of the GBP with various crises also does not get much coverage. I wonder is there a critical psychological point where this does become important. Crossing parity I think is something that would penetrate through to a headline. Maybe this 1€ having greater value than 1GBP would provoke some debate in Brexit?
~~DISCUSSION~~
Could Democracy & Our Market System Save Us From Ourselves?
~~META: date created = 2016-12-02 ~~
If technological advance is not an absolute good and it is instead precisely technological advance (Nuclear weapons, AI or some other version of Nick Bolstrom's black ball from the Urn) that will bring about our ultimate demise, then what can bring an end to this? Kaczynski would say there is nothing that can halt this advance in our current system without some type or revolution to overthrow our current institutions. Our ever rational drive to higher efficiencies & productivity cannot be stopped through any intellectual endeavor. Can our big brains that drive us towards ever more technological advance be our own undoing as in Vonnegut's Galápagos? Can we truly stay that we are driving technology for our greater good and not just for its own sake? Do the technologists do their work for the greater good of all humanity or merely because they are driven to do so as it is who they are? Being one of them, I suspect the latter,
But could the solution to the problem on how to halt or regulate technological process be already built into our current democratic, market system? In our current system, technological progress allows a certain small group of people who are skilled in these arts of pushing this technology to prosper disproportionately to the rest of the population. This causes economic imbalances over time that will cause some type of democratic unrest and rise anti intellectualism against the people who have more. Here the people reject the dogma of technological progress at all costs. (Trump's “post fact” victory in the US as a positive example to save humanity… I am potentially reaching a little bit here… ;) )
This somehow agrees with the view that through democracy the wisdom of the the people comes through - even if this does not happen every time, errors will be recognized and corrected. The typical disdain for democracy shown by intellectual elites (see for example H.L Menckens - “Notes on Democracy”) is based on the argument that the common man is too stupid to understand the complex issues of the day. It may however be that the intellectual elites are defining and pursuing particular issues that may not be relevant or indeed beneficial for everyone. The hope is, that on a long enough timeframe, people can recognize what is in their own best interests and this may not be aligned with the logic of what a small number of intellectuals would like to do. Recognizing what is in your best interest may not be an intellectual endeavor but one of low level preference.
Maybe stupidity is indeed a virtue, and it is maybe humanities stupidity that will allow us to keep our humanity, meaning our flawed, inefficient, unproductive ways at the center of our world instead of being pushed ever more to the edges by technology's rational.
~~DISCUSSION~~
Commerce and politics have always been sources of dramatic change - why is this always surprising?
Draft - Work in progress
People seem to be pre-programmed to accept the current status quo as eternal. Change is not something that is intuitively easy to grasp. It seems incompressible that the current nation states can crumble despite millennia of history to the contrary. No state structure lasts forever, no matter how big or how powerful it becomes. On an even shorter timeframe, the rise and fall of political parties can catch people fully unawares. After a few decades of one or other party or viewpoint completely dominating a political landscape, a few short years later this can all be swept away. This is sometimes for good - but with many notable examples where this was catastrophic.
It is also equally hard to imagine that some of the world's largest companies with enormous power and capital can disappear in a generation (and sometimes much more quickly). Why is this so hard to imagine despite all evidence to the contrary? Companies typically survive less than 25 years in the SP500.
Could the German automotive industry disappear in a decade? What consequences would this have both economically and politically in Europe? Consider the recent case of the all dominating Finnish mobile phone maker Nokia that had complete dominance over this market, massive quantities of funding for R&D and every advantage to maintain their dominance. However in the space of half a decade - they have been swept aside. A similar fate for Blackberry.
~~DISCUSSION~~
Collecting My Notes as a Blog
Gathering my notes into a blog type structure following tips given on the dokuwiki site. This is of course a little meta in using the newly installed blog software to document how to do that, but yeah…Looks interesting how it gathers the notes together.
In the sea of data that is available in the world today, whatever I write here is essentially for my own amusement as it is unlikely that there is much that can appear online that has not already been said. Maybe we are already living in a world now like that envisaged by Jorge Luis Borges in his short story The Library of Babel in which everything has presumably been written and documented, but all that may be of value is buried amongst so much nonsense.
Winter won't last forever and I am sure the number of notes will decrease as temperatures rise again.
~~DISCUSSION~~~~DISCUSSION~~
Probability & Statistics
Reading “The Undoing Project” by Michael Lewis at the moment about the relationship and work of Daniel Kahneman and Amos Tversky. There are some examples given of how knowing the underlying probability or base rate of an event and given some initial sampling you can forecast the likely result for your total sample. Bayes Theorem is one tool to look at this and it yields some unexpected results that can differ substantially from the underlying probability due to the small sample size. This seems interesting and important as a lot of sampling is limited and so these outcomes are everywhere. How probabilities can be updated as new information comes in is also interesting. I am pretty sure I have learned this before but I think I will look at this again to understand it's full significance.
Looking again into the world of chance. Below is a work in progress…
Expressing Likelihood: Odds & Probability
Probabilities of an event can be stated as percentages or as a decimal with values between $0$ (won't happen) & $1$ or $100\%$ (certain to happen). Another way of expressing such probabilities is the odds for and against an event. Odds reflect the ratio of an event occurring or not $$Occurance: Non\mbox{-}Occurance$$ where the event will be clearly decided, i.e. one of the options must occur $$Occurance + Non\mbox{-}Occurance=1$$
For example 9 to 1 on - states the event happening is $9$ times more likely to happen than not to happen $1$. This corresponds to a probability of $90\%$.
To convert from probability to odds
$$ Occurrence \mbox{ to } (1 - Occurance) = Non\mbox{-}Occurance$$ So if the probability is 10% or 0.10, then the odds are $0.1$ to $(1-0,1) = 0.9$ or ‘1 to 9’ or '1/9' or '1:9' on.
To convert from odds to a probability
$$\frac{Odds \mbox{ } on}{Odds \mbox{ } on + Odds \mbox{ }against}$$ So to convert odds of 1/9 to a probability, using above relation 1/(1+9) to obtain the probability of 0.10 or 10%.
Betting odds
Fractional odds are using in UK/Ireland in the form of
- Profit/Stake.
Example 7/4 - means you will achieve 7€ profit for 4€ stake (Total of 11€ (7+4) returned upon winning). These odds are always given in integer form, however not always with lowest denominator to facilitate comparison between different odds e.g. 3/2 given as 6/4 to allow easy comparison with 9/4.
Betting odds include the profit to the bookmaker in addition to the underlying probability.
Decimal odds Total Return (profit+Stake) :Stake. In fractional even odds 1/1 becomes 2.
~~DISCUSSION~~
Combining Events & Conditional Probability
If event $A$ and event $B$ are independent, then $$P(A \mbox{ and } B) = P(A \cap B) = P(A) \cdot P(B) \label{indepprob}\tag{1}$$ Bayes equation is only relevant in situations when the events are dependent, i.e. conditional probability. If $A$ happening is dependent on $B$ happening first, then $P(A | B)$ is the (conditional) probability that you'll see $A$ if you're already seeing $B$. e.g. The probability of getting wet depends on whether or not it's raining. $$ P(A \cap B) = P(A|B) \cdot P(B) \label{condprob}\tag{2}$$ Consider the chances of getting sick when there is a contagion in the local population. If half the people are sick and the probability of you catching the disease if in contact with a sick person is $20\%$, then the probability of a random person having the disease is: $$P(B) = 0.5$$ and the probability of you catching it from them once in contact with them is: $$P(A|B) = 0.2$$ then the probability of you getting sick using equation ($\ref{condprob})$ is: $$P(A \cap B)= 0.5 \times 0.2 = 0.1 = 10\%$$
Also note, if the sick people are either not contagious then $ P(A|B) =0 $ or you do not come into contact with sick people $ P(B) =0 $ then it follows that $ P(A \cap B) = 0 $ and there is no chance you get sick!
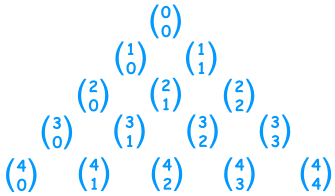
Permutations & Combinations
Picking $k$ items from a total of $n$ options, how many variations are there? The different ways of distributing k successes in a sequence of n trials.
Permutations - order does matter $$ P(n,k) = \frac{n\,!}{(n-k)\,!} $$
Combinations - order doesn't matter: $$ C(n,k) = \binom{n}{k} = \frac{n\,!}{(n-k)\,! k\,!} $$
This is also known as the binomial coefficient and the terms for different $n$ & $k$ can be seen graphically in Pascal's_triangle where the rows are numbered $n=0,1,2,3..$ and $k$ increasing left to right in each row $(0,1,2,3,\ldots)$

 5)
5)
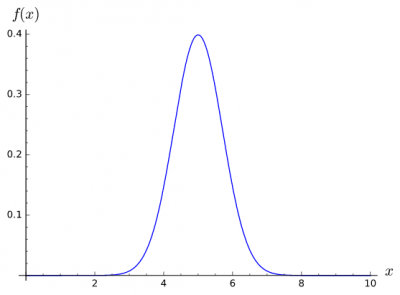
Bernoulli series, Binomial & Gaussian distribution
Building on the ideas of combinations, you can look at processes that have either single trials with multiple outcomes or multiple trials with a limited number of possible outcomes. An example of the latter, where the outcomes of each trial is binary (yes or no, 0 or 1) is known a Bernoulli process. The with general form or this is given be the Binomial_distribution.
A coin flip is an example of a process with only 2 outcomes (heads or tails) and so is a Bernoulli process. A series of n flips or Bernouli trials and the probability of any particular outcome for a coin can be calculated using Binomial (fair or unfair) can be calculated using the binomial distibution formula
What's the probability of getting 3 heads and 7 tails if one flips a fair coin 10 times.
You do $n=10$ trials. The probability of success in any given trial is $p=\frac{1}{2}$. You want k=3 successes (heads) and $n-k=7$ failures (tails). The probability is:
$$ P(n,k,p) = \binom{n}{k} p^k (1-p)^{n-k} \\ \binom{10}{3} \cdot \bigg ( \frac{1}{2} \bigg )^3 \cdot \bigg ( \frac{1}{2} \bigg )^7 \\ 120 \cdot \bigg ( \frac{1}{8} \bigg ) \cdot \bigg ( \frac{1}{128} \bigg ) = \bigg ( \frac{15}{128} \bigg ) = 0.117 = 11.7\% \\ $$
You want $k$ successes (probability: p^k) and n−k failures (probability: (1−p)n−k). The successes can occur anywhere in the trials, and there are (nk) to arrange k successes in n trials.
The binomial distribution $P(n, k, p)$ is approximately normal or Gaussian with mean $np$ and variance $np(1 - p)$ for large $n$ and for $p$ not too close to zero or one.
$$ f(x| \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x-\mu)^2}{2 \sigma^2}} $$
Where:
- $\mu$ is mean or expectation of the distribution (and also its median and mode).
- $\sigma$ is standard deviation
- $\sigma^{2}$ is variance
Bayesian Vs Frequentist
If the fairness of the coin is not known, then the probability for heads (success) $p$ is unknown. From from a fixed set of trials the fairness of the coin could be determined to a certain confidence level. The larger the sample the better the confidence level. The probability can be updated after each successive trial.
There is then a Frequentist approach which does not take prior experience into account or a Bayesian approach which does take prior experience into account in the form of a prior likelihood function.
https://en.wikipedia.org/wiki/Checking_whether_a_coin_is_fair
updating probabilities as new information comes in..
Consider a family planning to have 5 children. What is the probability of them all being girls? These are 5 independent Bernouli trials with a $50\%$ probability for each trial. Expanding on the equation ($\ref{condprob})$ for independent trials then: $$P_{All Girls} = 0,5^5 = 3.1\% $$ While if you already have $4$ children who are all girls… then the chances of having $5$ girls become $50\%$. With the additional information provided by the birth of the 1st $4$ children the probabilies of having $5$ girls rises considerably. New information changes the probabilities. This in some ways sounds obvious but is the basis of many statistics based problems - e.g. The Monty Hall Problem
Bayes' Theorem
$$ P(H|E) = \frac{ P(E|H) \cdot P(H) } { P(E) } $$
$H$ stands for any hypothesis whose probability may be affected by new evidence $E$ which corresponds to new data that were not used in computing the prior probability. $P(H)$
http://www.austintek.com/bayes/
- $P(H∣E)$ , the posterior probability, is the probability of $H$ given $E$ i.e., after E is observed. This is what we want to know: the probability of a hypothesis given the observed evidence.
- $P(E∣H)$ is the probability of observing $E$ given $H$. As a function of $E$ with $H$ fixed, this is the likelihood – it indicates the compatibility of the evidence with the given hypothesis. The likelihood function is a function of the evidence, E while the posterior probability is a function of the hypothesis, H.
- $P(E)$ is sometimes termed the marginal likelihood or “model evidence”. This factor is the same for all possible hypotheses being considered (as is evident from the fact that the hypothesis H does not appear anywhere in the symbol, unlike for all the other factors), so this factor does not enter into determining the relative probabilities of different hypotheses.
The factor $\frac{P(E|H)}{P(E)}$ can be interpreted as the impact of the evidence $E$ on the hypothesis $H$. Often there are competing hypotheses, and the task is to determine which is the most probable.
Bayes' Theorem - Examples
From “Thinking Fast & Slow” Chapter 6 - example given without good explanation. Happily, I found an explanation here.
Restate the problem: There is a city with 85\% green cabs & 15\% blue cabs and there is an accident where a witness identifies that the cab involved was blue. We are told that witness reliability in these cases is 80\%. What is probability that car was blue?
The example is posed to show the effect of ignoring the baseline probability. If there was no witness - then the chance of the care being blue would be 15\%. However with the witness involved, the temptation is to ignore this baseline and focus on the 80\% reliability - which is needless to say a mistake.
Formulate the question:
Hypothess $H$: Cab is Blue given the evidence $E$ that the witness reported this.
What is the probability of the cab being blue given that the witness identified (ID) it as blue (B) - $P(B∣IDB)$
$$ P(B|IDB) = \frac{ P(IDB|B) \cdot P(B) } { P(IDB) } $$
Breaking this down - $$ P(B) = \mbox{Probability of the car being blue} = 0,15 $$ $$ P(IDB|B) = \mbox{Probability that the cab would be ID'd as blue if the car was blue} = 0,8 $$
Then are left with the last term $P(IDB)$. We know that the events B and G are exclusive and cover all possibilities for the cab (the cab is Blue or Green), then:
$$ P(IDB) = P(IDB∣B) \cdot P(B) + P(IDB∣G)\cdot P(G) \\ = 0.8 \cdot 0.15 + 0.2 \cdot 0.85 = 0.12 + 0.17 = 0.29 $$ $$P(IDB|B) = \frac {0,8 * 0,15} {0,29} = 0,41$$
What happens in the case that you have more than one witness.
- $P(A)$, the prior, is the initial degree of belief in A.
- $P(A|B)$, the “posterior,” is the degree of belief having accounted for $B$.
- the quotient $P(B|A) / P(B)$ represents the support B provides for A.
- $P(A)$ and $P(B)$ are the probabilities of observing $A$ and $B$ without regard to each other.
- $P(A | B)$, a conditional probability, is the probability of observing event $A$ given that $B$ is true.
- $P(B | A)$ is the probability of observing event $B$ given that $A$ is true.
Suppose a drug test is 99% sensitive and 99% specific. That is, the test will produce 99% true positive results for drug users and 99% true negative results for non-drug users. Suppose that 0.5% of people are users of the drug. If a randomly selected individual tests positive, what is the probability that he is a user?
- 1000 individuals are tested,
⇒ there are expected to be 995 non-users and 5 users. ⇒ From the 995 non-users, 0.01 × 995 ≃ 10 false positives are expected. From the 5 users, 0.99 × 5 ≈ 5 true positives are expected. ⇒ Out of 15 positive results, only 5, about 33%, are genuine.
Technology, AI & Distribution of Capital
~~META: date created = 2016-11-20 ~~
Recent topics I read that I found interesting was a discussion regarding Artificial Intelligence (AI), super-intelligence and the so called singularity6) as well as other articles that question if technological advance is a positive force that can be controlled. Even in its most extreme from as expressed by Ted Kaczynski(better known as the Unabomber) there is still a logic to at least some of his thinking with respect to technological progress that is hard to ignore even though the conclusion he draws are more than just troubling (not to mention his actions).
Other topics I have been reading about are income distribution and inequality - notably Thomas Picketty's Capital in the Twenty-First Century. These topics of wealth distribution are Inextricably linked with financial independence and your place in society. Alternatively, like in Henry Thoreau's Walden, you can drop out of society and so massively reduce your expenditure and in this way achieve financial independence. It is remarkable that a story of a guy living in a hut and just taking care of himself can make the impression of being somewhat subversive in today's world.
As for long form writing - I am also reading the ultimate long form writing in Marcel Proust's “In Search of Lost Time”. Given the economic and class structure Proust writes about, this may not entirely unrelated to a world that Picketty would say we are returning to.
~~DISCUSSION~~
Monetizing positive impulses
Fundamental positive human impulses and desires are being often targeted as market opportunities. Three interesting recent examples are the desire for social contact (social media companies), desire for good food (Bio, organic companies) and the desire to live a healthy life (fitness wellness companies). All 3 areas are getting a lot of focus in recent years due to the huge potential. These desires are not limited to any one demographic group.
You could argue that the market economy is merely responding to a need in the market and fulfilling it. The question is how far the market helps the fulfillment of these desires or if it in fact twists them to the possible detriment of the very customers they are supposed to be serving.
Take bio/organic food for example. You can argue that there is a qualitative difference in the food and I believe this was the original trigger for this movement, but once it was discovered that people are prepared to pay significantly more for a simple, pure food then marketing gets to work. Simpler food, involving less processing and packaging could/should in fact cost less. Packaging your rice in non branded/unprinted hemp sacks appears however to increase the price dramatically.
Why then does somebody else just sell simpler for less. I am not sure. I am guessing there is a branding associated with the “simpler” product in these old style market style shops. Although people are nominally paying for a product that is a direct reaction to the heavily processed, heavily branded alternative product, the fact they are willing to pay more for these anti-brands would suggest they are in fact paying for this new form of branding.
~~DISCUSSION~~
Memories from Childhood
~~META: date created = 2016-12-03 ~~
Interesting article from the Atlantic - Traces of time lost7) about formation of memories in childhood and how memory and what type of memory affects us through our lives.
Pictures from our walk today in the fields close to our house today, which our two younger companions will presumably not remember - at least not like this. But then again, neither will I without the benefit of the picture…


~~DISCUSSION~~
Led Astray by the Media
Although I thought I always viewed media reporting sceptically, I have to admit that my world view recently does not seem to match what is actually happening and I wonder if I have been swayed by the media I consume. Examples where I was significantly surprised by recent happenings include the Brexit and Trump votes. I am also surprised that my expectation about what would happen if both of these events came to pass, as they have done, was also not correct. For example, electing a guy who espouses such rhetoric & potentially destabilizing ideologies like Trump, should have I thought led to instability, market uncertainty and drops in business confidence and equity prices. This expectation was apparently wrong as markets have rallied to all new highs after his election. Reality does not match up with my world picture. I am not sure why, but at least that much appears to be true.
Why is this the case and why I am not seeing it? Is it that the news and media that I am reading is so slanted and divorced from reality that I am even unaware of what is driving the real world anymore? Articles are still being written complaining about the electoral college/popular vote or of Russian hackers affecting election results. This seem to me to confirm that the media I am reading is drifting away from a neutral reporting of what is happening in the world and providing a super strong editorial bias for what they wish to be happening. Amazingly, I find myself agreeing with Trump camp statements saying that if the election went the other way, then complaints about Russians hacking emails and the rules of the electoral system would be considered fringe, crackpot conspiracy theories. If I flip it around - this is indeed how such articles appear. Why not accept your side lost and think about why? What message is coming from the electorate.
What explanation is there for markets responding so positively to Trump's election? What am I currently blind to?
~~DISCUSSION~~
View Source: – http://www.fashionusaonline.ru/
How I now do my reading - Instapaper & Kindle
~~META: date created = 2016-11-21 ~~
21 Nov 2016 - dob
I have started using Instapaper to gather long form articles I want to read and having them sent automatically on a weekly basis to my Kindle. My impulse is to get away from the 140 Character Twitter snippets of mostly ill thought out garbage and instead focus on long form articles that are properly structured and thought through. There is surely enough noise in the world already without adding more through twitter & other social media feeds. Reading this stuff feels like channel surfing on TV - where in the end your time is gone, you have not gained anything and you have not even particularly enjoyed it. If I am to put in the effort and time to read something, then I would hope that the writer has something interesting to say and has taken the time to write it properly.
I have found a way that I can quickly and easily access the text that I highlight while reading online at this link. The notes & highlighted text are uploaded using the kindle Whispersync function as far as I understand, so you need to have this option clicked in the kindle settings for this to work.
Taken together this allows me build up to a nice collection of articles that caught my interest over time as well as the key points in each article that grabbed my attention.
~~DISCUSSION~~
Achill
Stunning views on road to Keem Bay on Achill_Island, Co. Mayo.


…and now on to find something to interest myself in 2017. I plan to look closer into what is going on around me locally in 2017. Perhaps there are some new and interesting events and people to be discovered.
~~DISCUSSION~~
Archive Oveview
Blog History
2018
June
- 11 - Gold
- 11 - Erdős Number
- 11 - Emacs & Macros
- 11 - Currency Variation & Stock Price
- 11 - Could Democracy & Our Market System Save Us From Ourselves?
- 11 - Commerce and politics have always been sources of dramatic change - why is this always surprising?
- 11 - Collecting My Notes as a Blog
- 11 - Probability & Statistics
- 11 - Technology, AI & Distribution of Capital
- 11 - Monetizing positive impulses
- 11 - Memories from Childhood
- 11 - Led Astray by the Media
- 11 - How I now do my reading - Instapaper & Kindle
- 11 - Author Michael Lewis
- 11 - Achill