Table of Contents
Constant Growth / Inflation / Compound Interest
“The greatest shortcoming of the human race is our inability to understand the exponential function.” 1)
Compound interest and Inflation being two notable financial examples where consequences of a constant growth rate can be observed:
- Good investment: 15% growth over 5 years will double iniitial value
- Inflation: -4% over 50 years will eliminate 87% of value
Calculator
Set negative number for “Interest” to look at effect of inflation
Math
Calculator uses a formula assuming the interest is Compound annually (APR%):2)
$$ A = P \left( 1+r \right)^{t} \label{compound_annual}\tag{1} $$
where:
$A$ = amount of money accumulated after t years, including interest
$P$ = principal amount
$r$ = annual rate of interest (as a decimal)
$t$ = number of years the amount is deposited or borrowed for
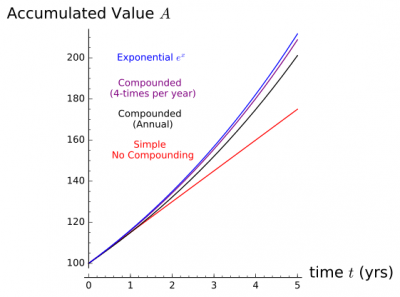
A broader overview of how you can describe constant growth can be found in the table below 3). The difference is essentially the interval used for compounding, from never (simple) to every instant (continuous growth $e^{r t}$).
| Term | Formula | Description & Usage |
|---|---|---|
| Simple | $$P \cdot (1 + r \cdot t)$$ | Fixed, non-growing return (bond coupons) |
| Compound (Annual) | $$P \cdot (1 + r)^t$$ | Changes each year (stock market, inflation) |
| Compound(n times per year) | $$P \cdot \left(1 + \frac{r}{n}\right)^{nt}$$ | Changes each month/week/day (savings account) |
| Continuous Growth | $$P \cdot e^{rt}$$ | Changes each instant (radioactive decay, temperature) |
where $n$ is the number of times the interest is compounded per year
Assuming a $15\%$ growth rate the below graphic demonstrates what the difference the different compounding intervals make over a 5 year period.
Other math based article on the topic.
Compounded Annual Growth Rate - CAGR
How to judge the performance of an investment that runs over a number of years with a different annualized rate of return each year? What is the Compounded Annual Growth Rate for a given starting & final value over a fixed time period? Rearranging equation $\ref{compound_annual}$ above:
$$r = \left( \frac{A}{P} \right)^\frac{1}{t}-1 \label{CAGR}\tag{2} $$
Given a number of years $t$ in which the starting principle $P$ has grown to the final accumulated value $A$, then equation $\ref{CAGR}$ provides you with the Compounded Annual Growth Rate (CAGR) for this period.